TUGAS 2 LOGIKA FUZZY

[REVIEW] FUNGSI KEANGGOTAAN HIMPUNAN FUZZY- REPRESENTASI KURVA LINEAR, KURVA SEGITIGA, KURVA TRAPESIUM DAN KURVA LONCENG BETA

Assalamulaikum wr,wb.

Hiiii teman-teman. Dapet lagi ini tugas kedua untuk mata kuliah logika fuzzy dari dosen kita ibu kurnia. Kali ini tugasnya masih sama kayak yang kemaren sih [meriview] tapi kali ini kita meriview [kurva] yang telah dipelajari minggu kemarin diperkuliahan. kelompok kita juga dapat tambahan review satu kurva lagi yaitu kurva lonceng beta. Untuk lebih memahami tugas minggu lalu kami telah meriviewnya sedimikian rupa, semoga dapat dipahami dengan mudah ya.. J

Apa itu Fungsi Keanggotaan ?

Fungsi keanggotaan (membership function) adalah suatu fungsi yang menunjukkan pemetaan titik titik input data ke dalam nilai keanggotaannya.

Untuk lebih paham lagi kita langsung coba jelaskan langsung dengan contohnyaa yah. Pertama - tama untuk membuat fungsi keanggotaan yang kita lakukan adalah mementukan beberapa semacam syaratnya terlebih dahulu seperti dibawah ini :

1. Variabel Fuzzy
   Disini kita pilih variabel apa yang akan kita bahas, misalnya “Lingkar Pinggang”
   
2. Himpunan Fuzzy
   
   Himpunan Fuzzyadalah himpunan yang tiap elemennya mempunyai derajat keanggotaan tertentu terhadap himpunannya.Didalam himpunan fuzzy terdapat dua atribut linguistik dam numeris, Atribut linguistik adalah penamaan suatu grup yang mewakili suatu keadaan atau kondisi tertentu dengan menggunakan bahasa alami. Sedangkan atribut numeris adalah suatu nilai (angka) yang menunjukkan ukuran dari suatu variabel.
   
   Contoh : Kecil, Sedang dan Besar
   
3. Himpunan Semesta
   
   Himpunan fuzzy yaitu suatu grup yang mewakili suatu kondisi atau keadaan tertentu dalam suatu variabel fuzzy. Contohnya: Kecil, Sedang dan Besar pada lingkar pinggang. Sedangkan semesta adalah aitu keseluruhan nilai yang diperoleh untuk dioperasikan dalam suatu variabel fuzzy, semesta pembicaraan merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri kekanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi batas atasnya.
   
   Contoh : semesta pembicaraan untuk variabel lingkar pinggang [61 86]
   
4. Domain
   
   Domain adalah keseluruhan nilai yang diijinkan dan boleh dioperasikan dalam suatu himpunan fuzzy.
   
   Contoh :
   

   
   

      Kecil [61  68,5]

   
   

      Sedang [71  78,5]

                  Besar [81  86]
   
5. Representasi Linear
   
   Terdapat tiga representasi yang sederhana dan sering digunakan dalam analisis himpunan fuzzy, yakni representasi secara linier, segitiga, dan trapesium. Dalam representasi linier, memetakan input crisp ke derajat keanggotaannya dapat digambarkan sebagai suatu garis lurus. Terdapat dua keadaan himpunan fuzzy yang linier.
   

Nah ini nih beberapa kurva yang akan kita review ditugas kali ini, yuk kita sama - sama belajar beberapa kurva yang kita review beserta contohnya...

1. Kurva Linear
   Ada dua representasi linier, yakni representasi linier naik dan representasi linier turun. Representasi linier naik, yaitu kenaikan himpunan fuzzy dimulai dari daerah grafik yang memiliki nilai keanggotaan nol [0.0], yang selanjutnya bergerak ke kanan menuju ke nilai derajat keanggotaan yang lebih tinggi. Gambar berikut ini menunjukkan himpunan fuzzy naik.
   
   
   
   
   
   
Selain itu terdapat pula representasi linier turun, yaitu garis lurus yang dimulai dari nilai pada daerah dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak turun ke nilai pada daerah yang memiliki derajat keanggotaan lebih rendah. Gambar berikut ini menunjukkan himpunan fuzzy turun.



Contoh :
   Representasi linear naik ukuran lingkar pinggang
                     Kecil [61  68,5]                       Sedang [71  78,5]                    Besar [81  86]



Kemudian hitung derajat keangootaan masing-masing dengan rumus :
           

μ [x]  = (x-a) / (b-a)

          - Domain lingkar pinggang kecil
              
μ [62]  = (62-60) / (68,5-61)
= 2/7,5
                                    = 0,27
- Domain lingkar pinggang sedang

             μ [74]  = (74-71) / (78,5-71)

                         = 3/7,5
                         = 0,4

- Domain lingkar pinggang besar
           
            μ [85]  = (85-81) / (86-81)

                        = 4/5

            = 0,8

2. Kurva Segitiga
   Representasi segitiga, pada dasarnya adalah gabungan antara dua representasi linier naik dan turun. Gambar dibawah akan menunjukkan representasi himpunan fuzzy segitiga.
   
   
   
   Contoh :
                  Domain =      Sejuk [15  25]             Normal [20  30]        Hangat [25  35]

   
   

                Misalnya kita ambil nilai x adalah 21. Nilai 21 berada diantara a dan b. Maka menggunakan rumus :

   
   

   μ [x]  = (x-a) / (b-a)
   
   

              - Domain umur muda
   

   μ [21]  = (21-15) / (25-15)

   
   

   = 6/10

                                       = 0,6
   
3. Kurva Trapesium
   Kurva trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa titik yang memiliki nilai keanggotaan satu. Adapun persamaan untuk kurva trapesium ini adalah:
   
   
   
   Contoh :
                 Domain : Sejuk [15  25]   Normal [20  30]    Hangat [25  35]    Panas [30  40]

   

          Disini misalnya kita ambil nilai x untuk kategori normal adalah 28. Maka kita akan menggunakan rumus :

   
   
   

   μ [x]  = (d-x) / (d-c)
   
   

             - Domain suhu
   

   μ [28]  = (27-28) / (35-27)

   
   

   = 1/8

                                       = 0,125

   
   
   
   
4. Kurva Lonceng Beta
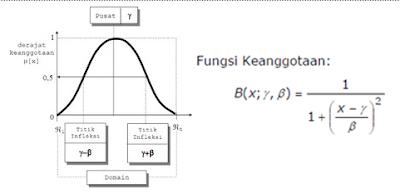
   Seperti halnya kurva PI, kurva BETA juga berbentuk lonceng namun lebih rapat. Kurva ini juga didefinisikan dengan 2 parameter, yaitu nilai pada domain yang menunjukkan pusat kurva (γ), dan setengah lebar kurva (β) . Nilai kurva untuk suatu nilai domain x, diberikan sebagai:
   
   
   
   Contoh :
                  Fungsi himpunan untuk parobaya pada variabel umur dengan domain :
   
   

   Parobaya [35  55]
   
   
   
   Kita misalkan x nya adalah 41 dan 53.                        Maka kita hitung dengan menggunkaan rumus seperti diatas :
   
   μ [41]  = 1/(1+((41-45)/5²)
               = 0,61
   μ [53]  = 1/(1+((53-45)/5²)
               =  0,28
   
              Jadi, didapatlah derajat keanggotaan untuk x 41 adalah 0,61 dan x 53 adalah 0,28.
   

Sekian duluu yaah man-teman pembahasan tugas kali ini, kayanya bakal ada lagi diminggu yang akan datang. Tetap semangat. Dan terimakasih sudah membaca J

References : http://www.zalora.co.id/womens-size

Posted by :

Ezy Claudia Nivsky   (G1A012026)

Helsi Tia Vermala    (G1A012048)

Eno Rahmandha        (G1A012070)